In the context of magnetic materials, the total magnetic energy of a system can be described from an appropriate physical model depending on the spatial scale. At micro down to nano-meter scales, micromagnetics can describe a magnetic material by approximating the quantum mechanical quantities of spin and orbital angular momentum of the atoms as a space dependent classical vector field known as magnetization. In particular, in ferromagnetic materials the magnetization field can describe different magnetic interactions that occur between atoms, such as the Exchange or dipolar interactions, or the interaction of the material with an external field, known as Zeeman interaction. Or even the intrinsic anisotropy of the ferromagnetic crystal. In the micromagnetic framework these interactions contribute to the total free energy of the material:
E = E_{\text{Zeeman}} + E_{\text{anisotropy}} + \ldots
Temperature effects in the energy can be approximated by scaling the interaction constants, which can be estimated experimentally. The magnetic system will stay in equilibrium at points of minimum energy with respect to the magnetization, i.e. at local energy minima (LEM). At a LEM the magnetization vectors will have a particular arrangement that lowers the overall energy of the system. For example, in sufficiently large ferromagnetic spheres the magnetization will form a vortex pattern that decreases the dipolar interactions.
The lowest energy point, i.e. the global energy minimum, is usually very difficult to find theoretically.
When considering temperature, thermal fluctuations make the magnetization vectors to randomly precess. This effect is better described with a semi-classical atomistic description of the system, by using a discrete lattice of magnetic moment vectors (generally referred as spins) rather than a continuum magnetization vector field. The dynamics caused by temperature cause that the system jumps between different local energy minima, if there is sufficient energy for the system to cross energy maximum regions known as energy barriers. Statistically, the system will favor to stay in regions of minimum energy, thus at the LEM points.
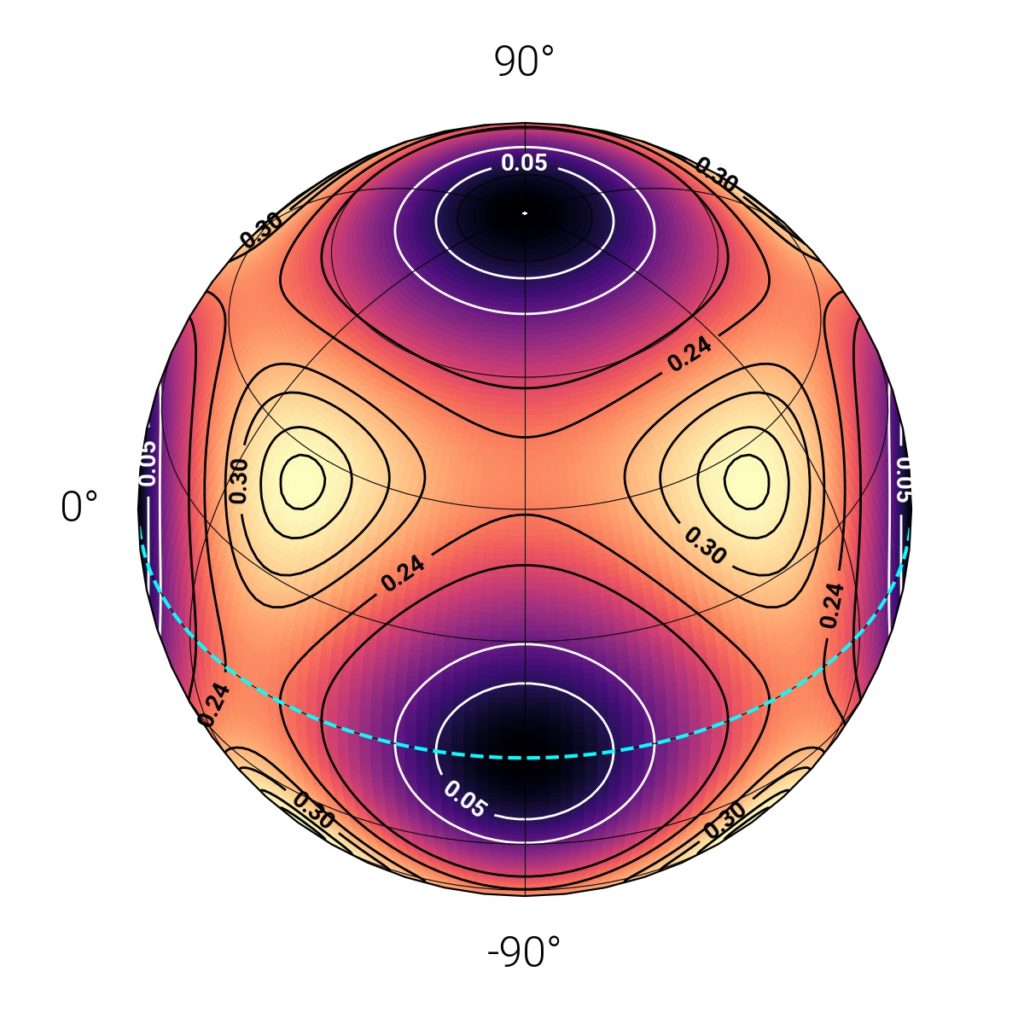
In the figure on the right we show a sphere made of a ferromagnetic material where only cubic anisotropy is considered as interaction. In this system all the magnetization vectors will point in a single direction (there are no other interactions), which is given by an azimuthal and a polar angle in spherical coordinates. The colors at the sphere surface indicate the energy (arbitrary units of the magnitudes at the contour lines) depending on the direction the magnetization field is oriented. The sphere can also be seen as the energy dependence of a single magnetization vector. The latitude at 0° (Equator line) is marked with a cyan dashed line. From the figure it can be seen that if the magnetization points to the poles (+z, -z) and at the +x, -x, +y, or -y directions, the energy is minimum, thus these points are LEM. Regions of maximum energy separating these local minima correspond to the energy barriers between the LEM.
REFERENCES
http://micromagnetics.org/micromagnetism/ [2] A. Aharoni. Introduction to the Theory of Ferromagnetism. Oxford University Press, 2000.




